Cross Site Public Lesson Study #5 - 6th Grade - The Border Problem
- Yay Math!
- Jun 22, 2020
- 7 min read
Over the 2018-2020 school years teacher teams from the Mathematical Agency Improvement Community (MAIC) Lesson Study Network conducted research lessons culminating (so far) in six public lesson study events. This post documents and memorializes the fifth lesson of the series – a 6th grade lesson using the Border Problem to explore how to set up algebraic expressions.
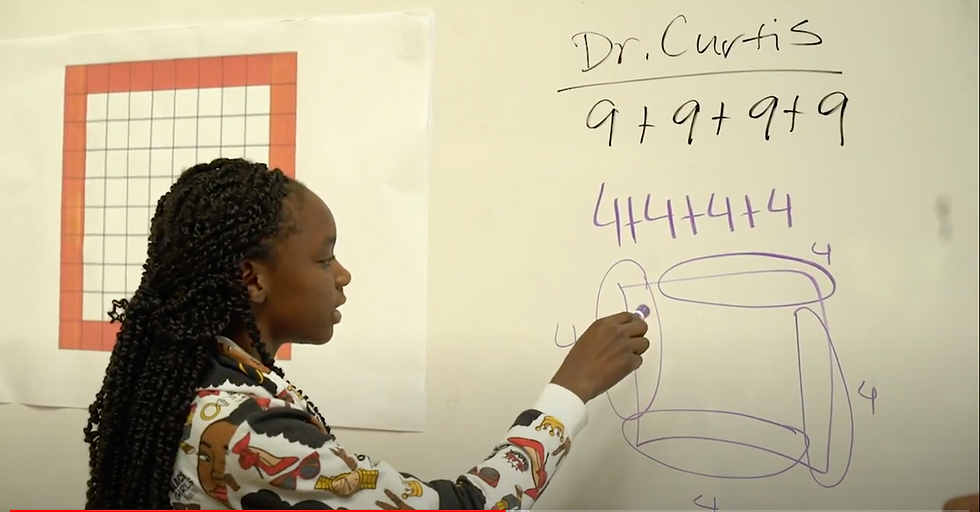
Why Lesson Study?
“Knowledge for teaching is embodied in instruction and is spread and refined as teachers watch and discuss practice” ~ Lewis & Hurd, 2011
In order to improve student learning, teachers need opportunities to observe student thinking and discuss teaching. Lesson study provides a structure for teachers to collaborate around pressing problems of practice and to engage in cycles of inquiry to explore the intersection of pedagogy and student learning. Engaging in lesson study supports educators in:
Developing pedagogical skills necessary to enact ambitious instruction in classrooms
Building the mathematical knowledge necessary to teach for student understanding
Crafting a communal vision of ambitious student-centered teaching for equity
What is a Research Lesson?
Lesson study can take many forms – quick lesson study cycles lasting 1-2 days to test a particular practice, or longer more in depth research lessons that explore more complex problems of practice. This post memorializes a 6th grade research lesson on creating algebraic expressions.
A research lesson is driven by a pressing problem of practice such as "how can we develop students' ability to engage in rich mathematical discussions, including listening to, building on, and challenging each other's ideas?" To explore the problem, the research team develops a mathematical understanding goal, an equity related teaching goal, and a theory of action to guide their inquiry. The team then designs a research lesson by researching best practices, exploring the standards and situating the lesson within the common core conceptual progressions, choosing focal students and anticipating student thinking.
During a research lesson, a teaching team introduces students to new learning, and tests out a new lesson structure, pedagogical move, or task, and collects data to determine how it impacted student learning and the development of an equitable learning environment. The lesson is observed by two outside individuals: a content commentator, and an equity commentator. The commentators provide feedback to the team about the degree to which the lesson achieved the research team’s content and equity goals.
The Research Team
The cross-grade level research team included:
Dr. Curtis Taylor, 6th Grade Math/Science, High Tech Middle Mesa
David Garcia, Preservice Teacher, HTH GSE/High Tech Middle Mesa
Dr. Kristin Komatsubara, HTH GSE Faculty
Yekaterina Milvidskaia, Improvement Coach HTH GSE
Dan Ryska, 9th Grade Math, Vista High School
Ruth Smith, 2nd Grade High Tech Elementary Mesa
Candice Weston, 6th Grade Math/Science, High Tech Middle Mesa
The team met for one hour a week for eight weeks to research and design the research lesson.
Public Lesson Study Event
The Pre-Brief
Memorializing Document (format adopted from a SFUSD & Mills College resource)
Video of the full unedited lesson can be found here. Edited videos for brevity and clarity are below.
This lesson took place March 6th, 2020 at the Forum at the HTH GSE. The following videos document portions of the pre-brief, the research lesson, and the post-lesson debrief, including commentary from the equity and content experts.
The Research Question & Theory of Action
The team developed a research question based on observations of student behavior and content knowledge from their contexts. How can we support students in trusting their own thinking and embracing the feeling of vulnerability in order to articulate their own and others thinking?
The research team shares their research question and theory of action.
They also developed a theory of action to guide their inquiry cycles:
If we as teachers pose questions with a variety of methods and interpretations and we honor each method through discussion and analysis, then students will see the value in diverse thinking, resulting in students feeling more open to sharing their thinking and listening to others.
The Context
Next the team shared the context for the lesson. What students were exploring in their current unit.
The research team shares the context for the problem.
Do the Math!
We have found it helpful to have the audience members attempt the math problem themselves before watching the lesson. This supports audience engagement and understanding as students work through the task. We encourage you to try it too
The math task!
The Mathematical Understanding Goal & Anticipating Student Thinking
Learning from a previous research lesson highlighted the importance of having a concrete mathematical understanding goal. The specificity of the content understanding goal has an impact on what can be learned from the research lesson. The more specific the content understanding goal, the easier it is to determine whether students meet the content understanding goal for the lesson. A common misconception among educators is that a standard is a mathematical understanding goal, the truth is that one standard is often made up of many different, critically important understandings that need to be "chewed" on multiple times and in different ways for students to develop a robust schema/understanding for the concept. In this case the team was focused on the second part of this mathematical understanding goal: Students will understand how a numerical expression can model a visual representation and use the structure within these expressions to generalize their expression (create an algebraic expression) in order to find the total number of squares for any figure number.
The team shares the mathematical understanding goal for the lesson.
The research team also anticipated how their focus students might approach the task, the connections they hoped to spark during the lesson, and the learning objectives for the lesson.
The team shares the anticipated student thinking for the lesson.
The team shares the learning objectives for the lesson.
The Equity Goal
The team also generated an equity goal for their lesson. Equity goals relate to the effectiveness of the classroom learning culture and patterns of student participation.
The team's equity goal: Through turn-and talks and whole class share outs, students will develop math flexibility by valuing each others’ ideas. Students will demonstrate value by listening to, questioning, and/or applying the math strategies of their peers.
The team shares the equity goal for the lesson.
Mathematical Practices
The Common Core outlines key mathematical practices that students should be developing to build their mathematical identities.
The research team outlined the practices focused on during this research lesson.
Data Collection & Assessing Student Thinking
For data collection, each team member (other than the presenting teacher) closely observed the thinking of one of their focus students throughout the lesson. By tracking how their focus student experienced the problem and what factors contributed to their learning. What did they think about during the independent work time? How did questions/ideas from peers shape their thinking? Any "a-ha" moments? These observational data are examined along with student work samples by the team during their debrief session.
The Research Lesson & Observation
Task Launch
The lesson was structured so that students were explaining their thinking and discussing the thinking of others. It started with a task launch followed by students sharing their strategies for how they figured out the number of squares in the border.
Launching the border problem.
One of the first challenges in the Border Problem is how to think about the corners in the border.
Students tackle the "corner issue".
Students share their strategies and document their numerical expressions.
Scaling the Figure and the Numerical Expressions
In order for the students to begin to see the underlying structure of their numerical expressions for calculating the border, they need to see how their numerical expressions change or stay the same for different sized figures. First the students scaled their expressions to solve for figure 100, then then scaled their expressions down to solve for figure 5.
Scaling up!
Scaling down to figure #5 and attending to underlying structure of the numerical expressions.
Generalizing & Lesson Close
During the final phase of the lesson, students were asked to think of an expression for any sized figure.
Students are prompted to attend to structure in the numerical expressions in order to create an algebraic expression for any sized figure.
The Debrief
After the lesson, the presenting teacher has the opportunity to reflect first on how the lesson went. Afterward, the research team engages in a discussion about how well they met their mathematical understanding and equity goals and what they learned about their research question and theory of action based on observations and data collected from focal students. In this public lesson Curtis and the team reflected publicly and the team also debriefed in a follow-up meeting, capturing their reflections in the memorialization document.
A research lesson debrief also includes commentary by an outside expert content commentator and equity commentator. In this lesson Dr. Elizabeth (Libby) Butler from San Diego Unified School District served as the content commentator and Bryan Meyer from Escondido Unified School District served as the equity commentator.
Curtis's Reflection
As the presenting teacher, Curtis reflects on how the lesson went and possible next steps.
Curtis reflects after the lesson.
The Research Team's Reflections
The team shares their reflections on the lesson.
Key Learnings for the Team
The team identified three key learnings about teaching and learning from the research lesson:
How to integrate the principles of Complex Instruction and recognizing and highlighting competence in the flow of a lesson.
The importance of slowing down in order to really understand student thinking
The importance and benefits of anticipatory planning in order to do both of the above learnings well.
Dr. Elizabeth Butler's Content Commentary
Dr. Butler shares her comments about the mathematical content and possible next steps to promote student learning.
Expert content commentator, Dr. Butler.
Bryan Meyer's Equity Commentary
Bryan Meyer comments on the team's equity goal.
Equity commentator Bryan Meyer.
Daisy Sharrock works at the Center for Research on Equity and Innovation at the High Tech High Graduate School of Education, and is part of a Student-Centered Learning Research Collaborative-sponsored research team that is currently engaged in the following study: Leveraging the Power of Improvement Networks to Spread Lesson Study. Read more about their current study here. We are grateful to JFF, KnowledgeWorks’, and the Student-Centered Learning Research Collaborative and its funders for their support. Learn more at sclresearchcollab.org

Comments